نسبت طلایی ، شماره های فیبوناچی و کسری ادامه دارد.

"الگوهای ریاضیدان ، مانند نقاش یا شاعر ، باید زیبا باشند ؛ ایده ها ، مانند رنگ ها یا کلمات ، باید به شکلی هماهنگ در کنار هم قرار بگیرند. زیبایی اولین آزمایش است: هیچ جای دائمی در جهان برای زشت وجود نداردریاضیات. "G. H هاردی

"در ریاضیات ، اگر الگویی رخ دهد ، می توانیم بپرسیم" چرا این اتفاق می افتد؟ ""چه چیزی را نشان می دهد؟"و ما می توانیم پاسخ این سؤالات را پیدا کنیم. "W. W. Sawyer

ریاضیات پر از الگوهای زیبا است ، توضیحات همیشه در آنجا اگر فقط بتوانیم آنها را پیدا کنیم و از وقایع یک ایده در بسیاری از زمینه های مختلف. دلیلی برای همه چیز در ریاضیات وجود دارد و ما باید سعی کنیم بدون توضیح از هر چیزی به طور کامل استفاده کنیم. اثبات در ریاضیات شامل یافتن پاسخ به سؤالاتی مانند "چرا این الگوی اتفاق می افتد؟"و "چه چیزی را نشان می دهد؟"

این مقاله چنین سؤالاتی را در رابطه با تعدادی از خصوصیات نسبت طلایی و توالی فیبوناچی ارائه می دهد و این خصوصیات را اثبات می کند. خواننده باید از زبان جبر و کنجکاو در مورد اینکه چرا نتایج ریاضی مانند آنها اتفاق می افتد خوشحال شود.

در حالی که این مقاله برخی از ایده های ریاضی قدرتمندی را که به طور گسترده در ریاضیات بالاتر استفاده می شود ، معرفی می کند ، هیچ دانش فراتر از سطح ریاضیات که معمولاً در سن شانزده سالگی در مدرسه بود ، لازم نیست. مقاله با یک روش عددی برای یافتن مقدار نسبت طلایی شروع می شود ، توضیح می دهد که چگونه اتومات های سلولی معرفی شده در Talk Talk گوسفند ، توالی فیبوناچی و نسبت طلایی را تولید می کند ، و در نهایت دنباله ای از بخش های مداوم را نشان می دهد و چگونه این موضوع را نشان می دهد. توالی به نسبت طلایی همگرا می شود. دو به دو ماتریس برای حل معادلات خطی همزمان استفاده می شود اما دانش قبلی از ماتریس لازم نیست.

یک روش تکراری برای ارائه مقدار عددی از نسبت طلایی $ phi $ توسط فرمول که نسبت طلایی را تعریف می کند ، یعنی $ $ phi = 1 + پیشنهاد می شود.<1over phi>$ $ تقریب اولیه $ phi_0 = 1 $ را بگیرید. برای به دست آوردن تقریب بعدی در دنباله $ phi_ $ ، فقط 1 را به متقابل تقریب قبلی $ phi_n $ اضافه کنید. فرمول $ $ phi_ = 1 + است<1over phi_n>، Quad phi_0 = 1. $ $ اولین اصطلاحات این دنباله عبارتند از: $ $ 1 ، 2 ، 1. 5 ، 1. overline 6 ، 1. 6 ، 1. 625 ، 1. 6154.$ $ و اگر چند اصطلاح دیگر این دنباله را محاسبه کنید ، متوجه خواهید شد که به سرعت به $ phi $ تبدیل می شود و به شش شکل مهم ، 1. 61803 ، فقط در سیزده مرحله و با مراحل بیشتر دقت بیشتری می بخشد.

این چه ارتباطی با دنباله فیبوناچی دارد؟خوب ، این دنباله ای از کسری است ، بنابراین فرض کنید $ $ phi_n =. $ $ سپس $ $ phi_ == 1 + = .$$ This is equivalent to $$eqalign < b_&= b_n+a_n cr a_ &= b_n .>$ $ راحت ترین روش برای نوشتن این جفت معادلات همزمان و محاسبه شرایط دنباله تولید شده توسط فرآیند تکراری که در اینجا شرح داده شده است ، استفاده از دو توسط دو ماتریس است. مزیت این است که ضرب توسط یک ماتریس دو دنباله اصطلاحات را در یک عمل محاسبه می کند. علاوه بر این ، ماشین حساب های گرافیکی این کار را به طور خودکار برای شما انجام می دهند. اگر مجبورید دوباره و دوباره و دوباره با همان ماتریس ضرب کنید.، این توسط یک قدرت ماتریس است ، سپس ماشین حساب قدرت را برای آن کار می کند و می توانید بسیاری از مراحل تکرار را با یک حرکت محاسبه کنید. خوانندگان می توانند این قانون را برای ضرب ماتریس در اصطلاحنامه بررسی کنند.$ $ pmatrix= pmatrix pmatrix $ $ اکنون که تکرار را انجام می دهد ، به یک ماتریس تبدیل شده است. ما می توانیم دوباره این کار را انجام دهیم:

and we can keep repeating this over and over again to give: $$pmatrix cr a_>= pmatrix ^n pmatrix $ $ اتوماتیک سلولی در مسئله href دنباله ای از کلمات حاوی فقط دو حرف A و B را تولید می کند. قانون این است که کلمه اول A است و برای به دست آوردن کلمه بعدی در دنباله شماقبل از آن ، هر یک را در کلمه قبل از آن به b و هر b به ab تغییر دهید. چند کلمه اول عبارتند از: A ، B ، AB ، BAB ، Abbab. بشرچند کلمه دیگر برای خود بنویسید و تعداد A و B را در هر کلمه حساب کنید. نوشتن $ a_n $ و $ b_n $ برای تعداد A و B در کلمه $ $ $ ، قانون تولید می شود: $ $ eqalign< b_&= b_n+a_n cr a_ &= b_n .>$ $ این همان جفت توالی است که در ابتدا در فرآیند تکراری استفاده می شود. جایگزینی $ b_ $ برای $ a_n $ در دوم این فرمول ها $ b_ = b_n+b_ $ نشان می دهد که توالی B دنباله فیبوناچی است که از 0 ، 1 شروع می شود. و به همین ترتیب می توان به راحتی نشان داد که دنباله A ، توالی فیبوناچی است که از 1 ، 0 شروع می شود. بنابراین ما دریافتیم که نسبت شرایط پی در پی یک توالی فیبوناچی $ a_/a_n $ ، که برابر با $ b_n/a_n است$ ، به نسبت طلایی همگرا می شود.

چگونه این با کسری ادامه می یابد؟خوب بیایید بررسی کنیم که چگونه تکرار $ phi_ = 1 + 1/ phi_n $ را تنظیم کردیم. ما با $ phi_0 = 1 $ شروع کردیم. اکنون مقادیر پی در پی $ phi_n $ را در فرمول تکرار جایگزین کنید ، دنباله ای از بخش های مداوم ایجاد کنید: $ $ eqalign< phi_0 &=1 cr phi_1 &= 1 + cr phi_2 &= 1 + <1over phi _1>= 1+<1overdisplaystyle 1+ < 1 over displaystyle 1>> cr phi_3 & = 1 +<1over phi_2>= 1+<1overdisplaystyle 1+ < 1 over displaystyle 1+ < 1over 1>>> cr phi_4 & = 1 +<1over phi_3>= 1+<1overdisplaystyle 1+ <1overdisplaystyle 1+ <1 over displaystyle 1+ <1over 1>>> >. >$ $ به وضوح می توانیم اصطلاحات بیشتر و بیشتر این دنباله را بنویسیم ، و بخش های مداوم طولانی تر می شوند اما کل دنباله توسط فرمول نقشه برداری $ $ phi_ = 1 + توصیف می شود.<1over phi_n>= <phi_n + 1 over phi_n>.$$

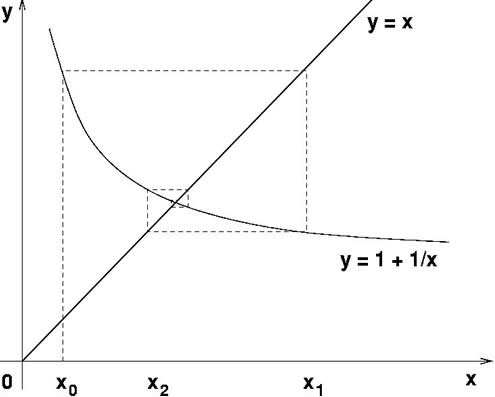
برای نشان دادن این که این دنباله نقشه ها باید همگرا شوند ، نمودارهای $ y = x $ و $ y = 1+1/x $ را در نظر بگیرند. اگر نقشه برداری $ x_ = 1 + 1/x_n $ تمایل به حد $ phi $ داشته باشد ، برای بسیار بزرگ $ n $ ، ما باید بتوانیم هر دو $ x_ $ و $ x_n $ را جایگزین $ phi $ کنیمدر نمودار در تقاطع $ y = x $ و $ y = 1 +1/x $ نشان داده شده است.

با استفاده از اولین تقریب $ x_0 $ ، یک خط عمودی را از طریق $ x = x_0 $ ترسیم کنید تا نمودار $ y = x+1/x $ را برآورده کنید که در آن ارزش $ $ به تقریب بعدی $ x_1 $ می دهد. بعدی یک خط افقی را از این نقطه بکشید تا به نمودار $ y = x $ با $ (x_1 ، x_1) $ ضربه بزنید. از این نقطه یک خط عمودی را برای دیدار با نمودار $ y = 1 + 1/x $ با $ (x_1 ، x_2) $ بکشید. برای یافتن تقریب بعدی یک خط افقی را از طریق این نقطه ترسیم کنید تا نمودار $ y = x $ را با $ (x_2 ، x_2) $ برآورده کنید. در این روش ، نمودار "Cobweb" را نشان می دهید و تقریب های نزدیکتر و نزدیکتر به نسبت طلایی $ phi $ نزدیک می شوید.

برای کسانی که می خواهند بیشتر الگوهای مرتبط و نتایج ریاضی را کشف کنند ، چالش ها و مقالات بسیاری در این وب سایت به تنهایی و هزاران نفر در جای دیگر در وب وجود دارد که با استفاده از هر موتور جستجو یافت می شود.

پروژه NRICH هدف از غنی سازی تجربیات ریاضی همه زبان آموزان است. برای حمایت از این هدف ، اعضای تیم NRICH در طیف گسترده ای از ظرفیت ها کار می کنند ، از جمله ارائه پیشرفت حرفه ای برای معلمان که مایل به انجام کارهای ریاضی غنی در تمرین روزمره در کلاس هستند.